LA SYMETRIE CELLULAIRE
***
LES ENSEMBLES REGULIERS
Nous avons vu jusqu'ici comment la symétrie cellulaire réalisait une structure relativement ordonnée à partir du chaos aléatoire. Paradoxalement, la même technique permet de créer de la variété à partir de suites ordonnées.
Au lieu d'affecter aux angles et aux rayons de l'ensemble générateur des valeurs aléatoires, on leur donnera des valeurs fonctions de l'indice.
* * *
LES SUITES ARITHMETIQUES
Le cas le plus simple est, dans le plan, un ensemble générateur ou les angles et les distances des axes augmentent d'une quantité constante ( dt pour les angles,dd pour les distances = fonction linéaire). Si "i" est l'indice on aura: pour l'angle t(i)=t(i-1)+dt, et le rayon d(i)=d(i-1)+d. Les axes forment alors une sorte de spirale d'Archimède. Malgré cette monotonie la symétrie cellulaire produit, dans des directions approximativement radiales, une succession de motifs à peu prés semblables mais de plus en plus grands et compliqués en s'éloignant du centre.


La figure de gauche montre le début d'une chaîne de parois au voisinage du centre et celle de droite l'image correspondante. Il apparaît nettement une structure périodique. La figure suivante (à gauche) montre l'évolution des motifs. Sur de plus grandes zones s'y ajoute une périodicité due aux symétries sur le dernier axe, formant des sortes de diabolo.


A la périphérie de l'ensemble (image de droite) on observe des bandes rectilignes de motifs égaux, perpendiculaires à la direction radiale.
Il suffit donc de deux paramètres: incrément des angles, incrément des rayons, tirés au hasard dans un certain domaine, pour obtenir une grande variété de formes, avec une structure binaire sous-jacente.
* * *
LES SUITES GEOMETRIQUES
Les angles augmentent encore d'une quantité constante, mais les rayons sont en progression géométrique: d(i)=d(i-1) x d (fonction exponentielle) ou, plus simplement, d(i)="d puissance i" ; "d" est la raison de la progression. Nous utiliserons la notation du BASIC c-a-d: d(i)=d^i.
Les axes sont alors tangents à une spirale logarithmique. Comme précédemment les motifs s'organisent dans des direction radiales (en réalité des spirales très ouvertes) mais la structure répétitive est alors très régulière, évoquant une similitude interne. La source des images est un anneau très mince couvrant le polygone des axes du premier tour.

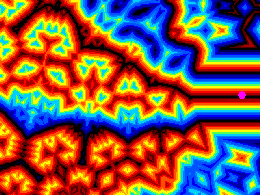
La structure sous-jacente, fondamentale, apparaît souvent clairement (à gauche). ce sont des arbres binaires spiralés de plus en plus ramifiés. La symétrie produit des enroulements de sens opposés mais le processus de SELECTION / ELIMINATION (voir 1° partie) évite que les branches voisines ne se chevauchent.
Dans certains cas les motifs évoquent des figures fractales classiques: arbres, Peano, Von Koch, Sipiersky... Dans le cas général il y a des combinaisons de courbes et de motifs symétriques plus ou moins compliqués, mais on peut toujours y retrouver les mêmes structures en arbre.




D'autres exemples sont dans la galerie SC-EXP.
Pour certaines valeurs des paramètres, on remarque des figures parfaitement géométriques (à gauche), en forme de polygones très caractéristiques. On peut y distinguer plusieurs cascades binaires en spirale.

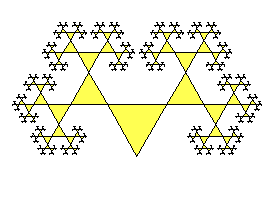
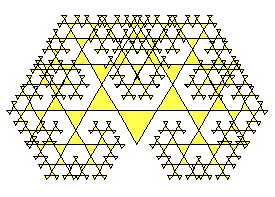
Un image analogue peut être calculée directement: c'est une cascade de triangles de dimension décroissant géométriquement (à gauche ). Mais si la "raison" est supérieure à d=0.618 il y a "enchevêtrement des branches" (à droite ), difficile à éviter dans le calcul. La SC supprime totalement le problème par sélection/élimination.
LA FORMATION DES STRUCTURES
Par construction, chaque axe forme avec le précédent un angle dt. Si dt est une fraction entière de deux pi, (dt=2 x pi/k), après un tour l'axe d'indice (i+k) sera parallèleà l'axe d'indice (i) et la structure sera très simple. Avec une fraction quelconque (dt=2 x pi/(k+e),e<1) il y aura "glissement de phase" et l'axe(i+k) fera avec l'axe(i) un angle ddt= e x dt. Le processus se reproduira ainsi périodiquement pour les tours successifs.
Rappelons que chaque symétrie supprime la moitié de l'image précédente. Si, dans le réseau des parois, on ne garde que ce qui subsiste des axes de l'ensemble générateur, sans figurer leurs répliques successives, on obtient une figure composée d'une suite ordonnée de quadrilatères disposés en spirale. Ils constituent un super squelette de l'image et sont tous semblables, de dimension croissante vers la périphérie.

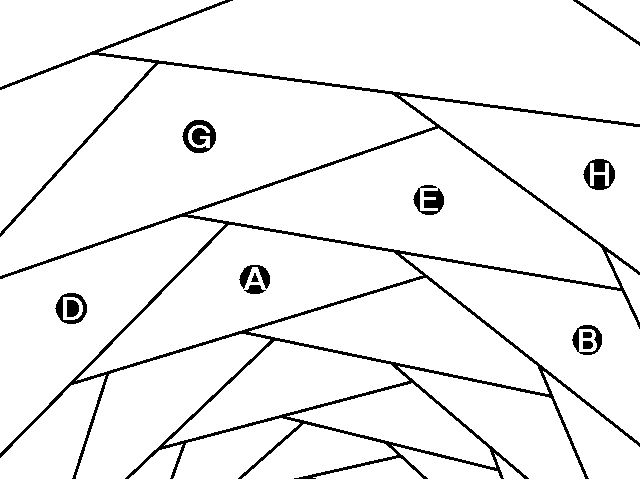
La spirale croit ici dans le sens des aiguilles d'une montre. Dans le fragment agrandi de droite le quadrilatère B suit le A. Les quadrilatères D et E proviennent du tour suivant, G et H d'un troisième tour. Ces quadrilatères ont leurs cotés opposés antiparallèles et leurs angles aigus sont dt et, selon le cas, ddt ou (dt+ddt).
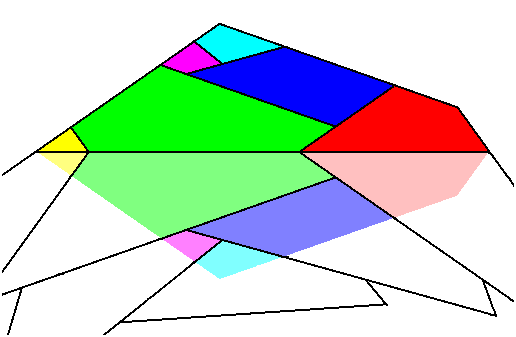
Comme le montre la figure, chaque quadrilatère (en couleurs vives) prélève par symétrie des fragments (différents) des quadrilatères précédents (en couleurs pâles). Il en résulte que cette transformation peut être vue comme une application du quadrilatère sur lui-même, un réarrangement ordonné mais compliqué des diverses zones avec contraction, symétries et duplications.
C'est l'occasion d'analyser comment s'organisent les motifs polygonaux:
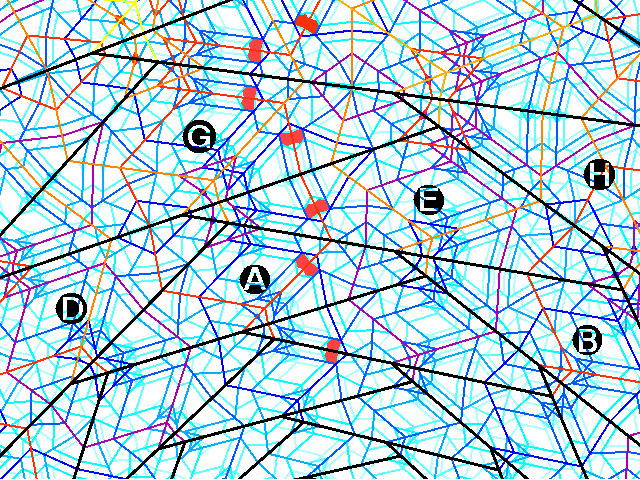
Par exemple, sur la figure de gauche le grand côté de A produit le symétrique du petit détail rouge (2 cellules) et du grand côté qui le porte (qui se retrouve parallèle au côté gauche de A). Après symétrie dans E ce détail se retrouve dédoublé dans G et l'un des deux a son axe parallèle au côté supérieur de G. Cet axe est parallèle et non confondu à cause de l'accroissement des dimensions. La symétrie sur la frontière de G reproduit le motif de la frontière de A, mais agrandi et plus détaillé. C'est ainsi que se concilie cette curieuse dualité: égalité des dimensions due à la symétrie et similitude des quadrilatères. Le petit motif en A va grandir, par accumulation successive et ordonnée, de détails identiques et produire le polygone caractéristique.
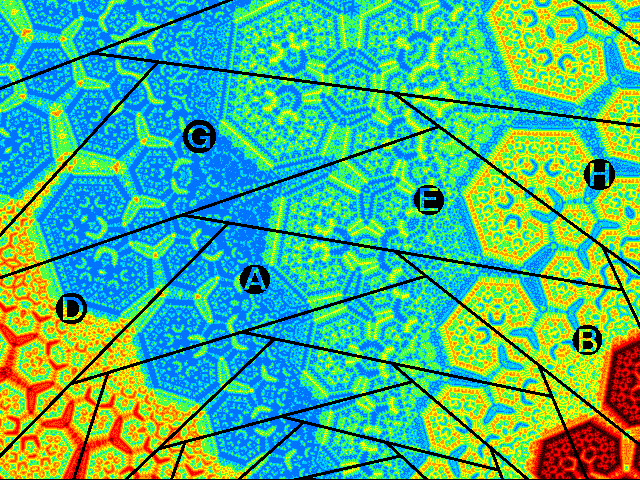
L'image de droite est obtenue après un plus grand nombre d'itérations, c'est à dire en augmentant le nombre d'axes vers le centre (une spirale logarithmique peut être prolongée indéfiniment dans les deux sens), pour multiplier les cellules (cela évoque une croissance naturelle). Cela produit la multiplication des détails. Remarquons qu'il serait équivalent (mais moins pratique...) de déplacer l'image vers l'extérieur sur l'écran et de rapetisser un quadrilatère de même orientation.
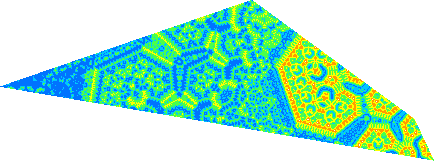
Notons que l'ensemble générateur des axes, parcouru en sens inverse, se rapproche assymptotiquement du centre. Théoriquement, avec un ensemble allant de d(1) tendant vers zéro à d(n) tendant vers l'infini, on pourrait couvrir tout le plan. Mais les cellules seraient alors infiniment petites...
Chaque quadrilatère (ici E) résume donc à lui seul l'ensemble de l'image (à la couleur prés). Cette similitude apparente doit être vérifiée: cela confirmera éventuellement le caractère fractal de ces ensembles.
Pour pousser l'analyse il convient d'effectuer une simplification radicale en choisissant une spirale, réduite à sa plus simple expression, dont les angles successifs différent de deux pi. On obtient alors une NAPPE d'axes parallèles. Avec deux de ces NAPPES, croisées sous un angle donné, le système permettra de produire des images plus démonstratives. Cette étude est particulièrement indigeste mais peut être consultée en note. Elle montre que la SC peut engendrer dans certains cas un objet fractal mais que c'est en général plus compliqué.
Les systèmesà deux nappes produisent des "chaînes" d'images répétitives.

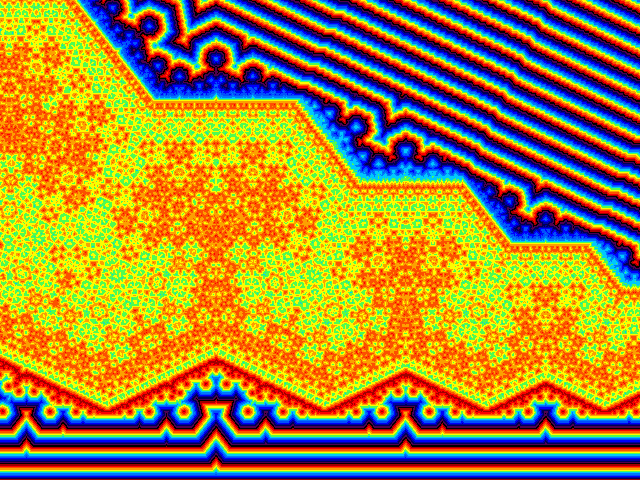
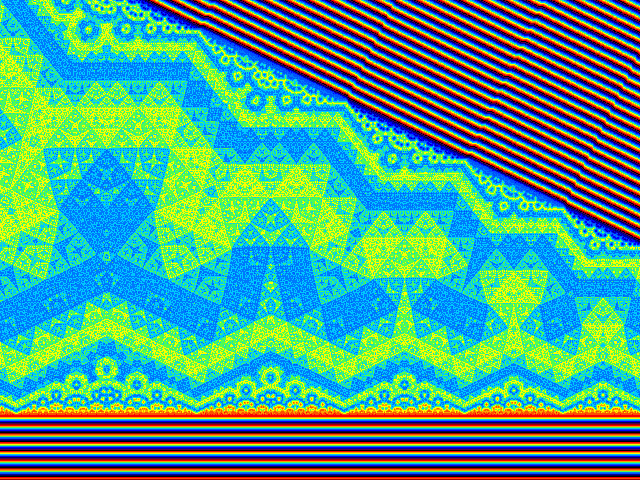



Elles présentent une grande variété en fonction de l'angle. Les images observées avec les spirales "normales" du début sont une combinaison de ces images élémentaires par l'enchaînement complexe des quadrilatères.
* * *
L'application de la SYMETRIE CELLULAIRE aux suites géométriques engendre des motifs très variés harmonieusement disposés, évoquant souvent des formes naturelles, quelquefois fractales. Elle semble constituer l'archétype de la SC.
Il suffit de deux paramètres, qui peuvent être choisis au hasard, pour engendrer une grande diversité d'images. On peut l'augmenter en remplaçant le "dt" constant par une alternance de deux dt légèrement différents.


Malgré tout, cette variété est limitée par la régularité due au "centrage" de l'ensemble généré. Il existe de nombreux moyens d'y pallier. Par exemple d'introduire quelques "défauts" au hasard dans la série des angles ou des rayons.
On rejoint alors le système des axes aléatoires évoqués dans la première partie. Il faut d'ailleurs noter que la fonction tangente adoptée au chapitre précédent pour la SC sphérique est proche, dans un certain domaine, de la fonction exponentielle.
A l'inverse il est possible d'introduire une certaine régularité dans ceux-ci: par exemple, après avoir défini une dizaine de droites , il suffit de reproduire ce groupe plusieurs fois en multipliant à chaque stade les rayons par un coefficient donné (c'est encore une croissance géométrique).

 .
.
Cela se révèle sur les images par des gerbes de petits éléments, de motifs binaires, analogues mais plus compliquées que celles des suites géométriques pures.
* * *
La page suivante proposera une autre application de la symétrie cellulaire. Une "greffe" de la SC sur la construction de fractales classiques permet de multiplier les possibilités de création d'images sur les ensembles réguliers.
Copyright © Hugues Amiard 2004 2008 Tous droits réservés.