LA SYMETRIE CELLULAIRE

note *

   Le point " p " génère le point " p' ", de couleur identique et situé de l'autre côté de l'axe et à la même distance . Le sens de la symétrie est défini par le CENTRE (point noir sur les schémas), situé du côté réfléchissant du miroir.

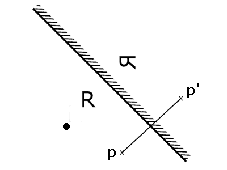
   Remarquons que le symétrique du caractère R est à l'envers; en effet une figure symétrique n'est pas égale mais inversée, bien que de même dimension (isométrie). Si on pliait la figure suivant la droite le point p' se superposerait exactement au point p.

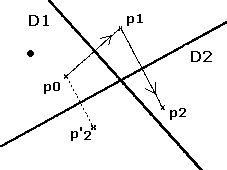
  Pour deux axes D1 et D2, le point p0 généré ,par symétrie sur D1, le point p1 puis, par symétrie sur D2, p0 génère p'2 et p1 généré p2 (figure de gauche). On obtient donc quatre points (avec trois opérations). Cette procédure n'est pas applicable en programmation car, avec "n" axes, il faudrait de l'ordre de "2 puissance n" calculs pour transformer chaque point du champ en reflets!... A vrai dire, dans le cours de cette itération, certains tomberont "derrière" un axe et seront supprimés. Mais beaucoup de ces symétriques se trouverons en dehors de l'écran ou confondus avec d'autres et presque tous ces calculs se révélerons inutiles.

   Il faut utiliser la méthode inverse (figure de droite): pour chaque pixel p2 de l'écran on recherche ses symétriques successifs sur les axes D, mais en commençant par le dernier D2. Si le symétrique est du côté du centre on continue l'itération sur ce point, sinon on l'ignore et on passe à l'axe suivant (c-a-d de numéro d'ordre inférieur). Le dernier point p0 tombe nécessairement au voisinage du centre et détermine, par exemple par ses coordonnées, la couleur du pixel p2. On peut vérifier sur le croquis que ce pixel est bien un reflet du point initial p0 de l'itération directe. Avec n miroirs, il ne faudra que n calculs par points de l'écran, ce qui est raisonnable en assembleur avec un calculateur rapide.

  Il est important de comprendre cette méthode fondamentale pour les applications qui vont suivre.